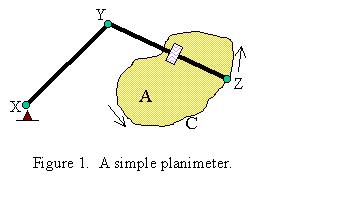
A Geometrical Explanation of the Polar Planimeter
On a bright sunny morning you sit at the breakfast table sipping your orange juice. Your very active puppy, needing attention after the long lonely night, jumps up on your lap and, splash!, the orange juice forms a puddle on the floor. In order to properly berate the naughty beast, you want to determine to extent of the damage, i.e., the exact area of the carpet that is now stained a yellowish-orange. Let's assume that the puddle's boundary is a simple closed curve C. By simple, I simply mean a curve which doesn't intersect itself (no figure eights allowed!) and which bounds a single connected region (measure distinct splash areas separately). Denote the area inside this curve by the letter A. The planimeter has an elbow at Y, a wheel on its arm YZ and a fixed pivot point at X.

I claim that the area A equals the length of the arm YZ times the circumference of the wheel times the number of revolutions that the wheel makes as you trace Z one full time around the curve C. It turns out that this is only true if X is outside the curve C and the arms XY and YZ never have to rotate past a full circle (you want the planimeter to be completely to one side of the curve, not surrounded by it).
The proof:
Let N be the number of revolutions of the wheel, counting counterclockwise as positive and clockwise as negative. Let L be the length of the arm YZ; let R be the distance between the elbow and the wheel; and let r be the radius of the wheel. Picture the region which the arm YZ passes over as its endpoint Z traces around the curve C. Let the boundary of this region minus the region inside C be denoted by C'. If the wheel turns counterclockwise, we'll say that YZ sweeps out positive area. If the wheel turns clockwise, we'll say that YZ sweeps out negative area. With this convention, the total area that the arm YZ sweeps out during a traversal of C is then the area bounded by (C+C') minus the area bounded by C', since the arm must backtrack over the region in C' in order to return to its starting position. This difference of areas is exactly the area A bounded by C, so now we just need to determine the total area swept out by YZ and that will be equal to A.
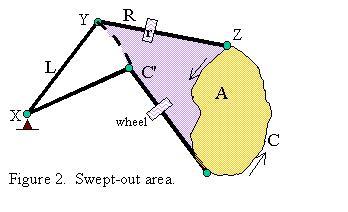
Move the arm YZ just a little bit, with the endpoint Z following along the curve C. Decompose this motion into two pieces, a translation and a rotation.
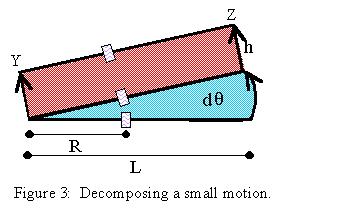
Let D be the distance the wheel rolls. When the arm YZ is rotating this distance will be R times the angle change dq, since the circumference of a sector is the radius times the angle. The area of a parallelogram is the height times the width, and the area of a sector of a circle is one half the angle times the radius squared. Now we can compute the area swept out by YZ during this small motion:
D = Rdq + h, so h = D - Rdq.
dA = L2dq/2 + hL = L2dq/2 + DL - RLdq = DL + dq(L2/2-LR).
Since the arm YZ returns to its original position, the total change in angle is zero. Therefore the total area A will equal L times D, where the total distance D that the wheel rolls equals the number of revolutions N times the circumference of the wheel.
A = (2prN)L.
Note that if you do have to find the area inside a figure eight, just measure each of the two regions separately and add the results together.
The geometric proof for this simple planimeter is adapted from that given by George Jennings in Modern Geometry with Applications, published by Springer-Verlag in 1994. This book contains several other such delightful applications, though the planimeter is my personal favorite.